
授業作家。
これまでに算数を中心に数多くの研究授業や公開授業の経験を積んできました。その中には全国大会や有料の研究会も含みます。
みんな大好きドミノピザ!一番お得なサイズはどれ?
以前、マクドナルドのジュースのS・M・Lでどれが一番お得かというのを紹介しました。
今日はみんなが大好きドミノピザ!でも、S・M・L、どれが一番お得か考えたことはありますか?
実は、この答えを導き出すのに、学校で習ったあの算数が役立つんです!
「単位量あたりの大きさ」も「円の面積」も、ただただ問題を解くだけではおもしろくありません。子どもたちが解きたくなるような課題にすることで、子どもたちは意欲的に取り組むことだと思います。
ほんの少しでいいんです。毎時間ほんの少しの工夫を積み重ねることが算数が好きな子どもたちを増やすためには大切だと考えています。
導入


(画像を見せる)

ピザだ!おいしそう!

右からSMLのサイズです。
問題
ドミノピザのS・M・Lサイズで最もお得と言えるものはどれですか。
※種類はマルゲリータで統一します。
条件
算数の問題において「条件」というのはとても大切です。条件1つで難易度を高くも低くもできます。また、条件1つで子どもたちの意欲を高めることも無くすことにもなります。なので、算数の問題を考えるときは条件をしっかりと考えることが大切だと言えます。
今回は、問題を解く際に必要な数値を伝えていません。これは、子どもたち自身に必要な数値を考えてほしいという願いからです。
ただし、クラスの実態において最初から数値を伝えるのはアリだと思います。そこは臨機応変にしていくことが大切ですね。
見通し

1枚あたりいくらか分からないと解けないよ・・・

ピザの大きさが分かれば・・・

そのためには直径の大きさが必要だね!
その他にも重さで考える方法もありますが、今回は円の面積の技能も使いたいので重さは扱いません。もちろん重さで考える方法も立派な発想だと思います。
単位量あたりの大きさをマスターしよう!
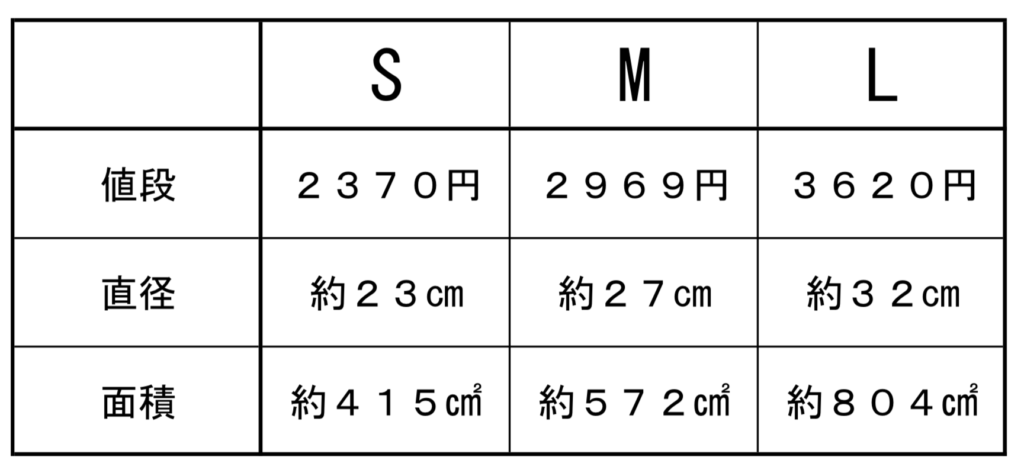
1円あたりの大きさ
S・・・415÷2370=約0.18㎠
M・・・572÷2969=約0.19㎠
L・・・804÷3620=約0.22㎠
1㎠あたりの値段
S・・・2370÷415=約5.7円
M・・・2969÷572=約5.2円
L・・・3620÷804=約4.5円
結論
Lサイズがお得と言える。
おわりに
今回はマルゲリータで統一して計算しましたが、もしかすると種類によっては結論が違うかもしれません。また、ほかのピザ屋についても計算してみないと分かりません。分かったことはドミノピザのマルゲリータはLサイズがお得だということです。
このように授業の題材に実際のピザ屋をもってくることで、子どもたちの意欲も上がり楽しく学習することへと繋がります。そして、自宅でデリバリーピザを頼む際には授業でやった内容を誇らしげにお家の人へと話すことでしょう。
今回のような題材は「話したくなる算数」と言えそうです。子どもが自宅で算数のことを話すことはプラスでしかありません。ほんの少しの工夫が大きなプラスへとつながるのです。








コメント