分数のわり算はひっくり返してかけ算
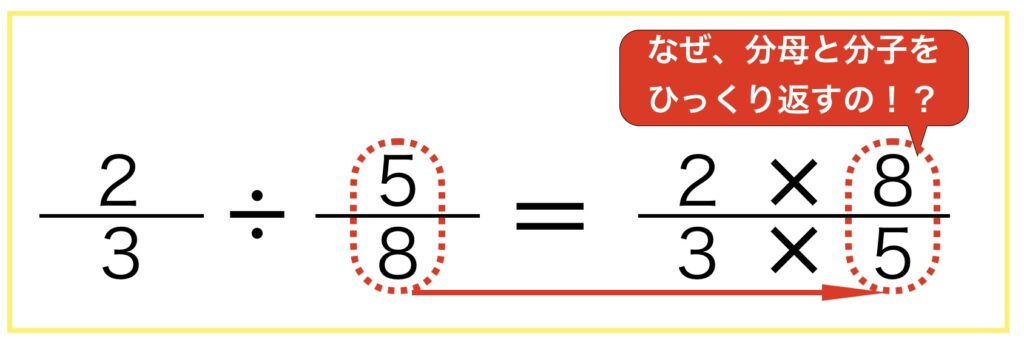
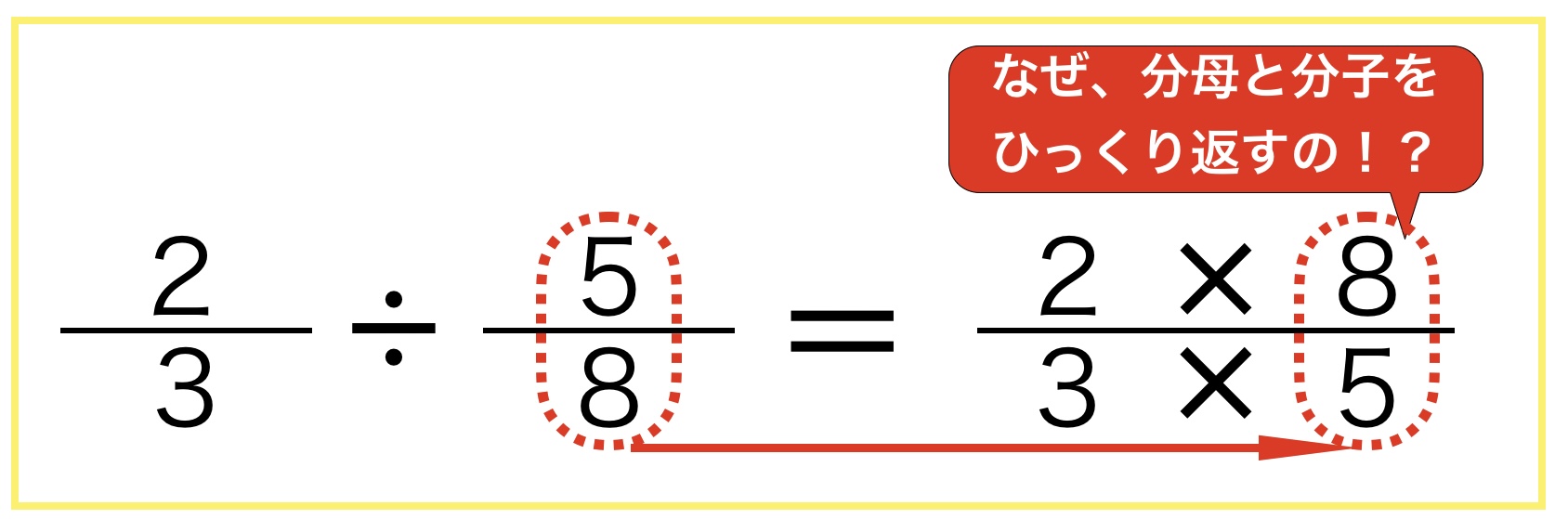
分数のわり算を計算する際に、分母と分子をひっくり返してかけ算することは多くの人が理解していると思います。
でも、なぜ分母と分子をひっくり返してかけ算するのか、その理由を説明できる人は多くはないでしょう。
もし、ここで子どもたちから「なぜ、分母と分子をひっくり返してかけ算するの?」と聞かれたときに果たしてどれぐらいの大人が説明できるのでしょうか。子どもたちの算数に対する素朴な疑問を、あやふやにするわけにはいきません。
さぁ、そこで今回は、分数のわり算をひっくり返してかけ算する理由を分かりやすく説明していきます。
結論
式を省略しているから。
分数のわり算をひっくり返してかけ算する理由
結論としては「式を省略しているから」です。
正確に式を書くとすると、本当はもっと式が長くなります。でも、毎回それを書くのは大変です。そのため、分母と分子をひっくり返してかけ算することで大幅に式を省略しているんです。
では、どのような式が省略されているのかを説明していきます。
わり算の性質
わり算の性質の一つに、「割られる数」と「割る数」に同じ数をかけても答えは変わらないという性質があります。この性質が、分数の割り算が分母と分子をひっくり返してかけ算に変換される理由と関連しています。
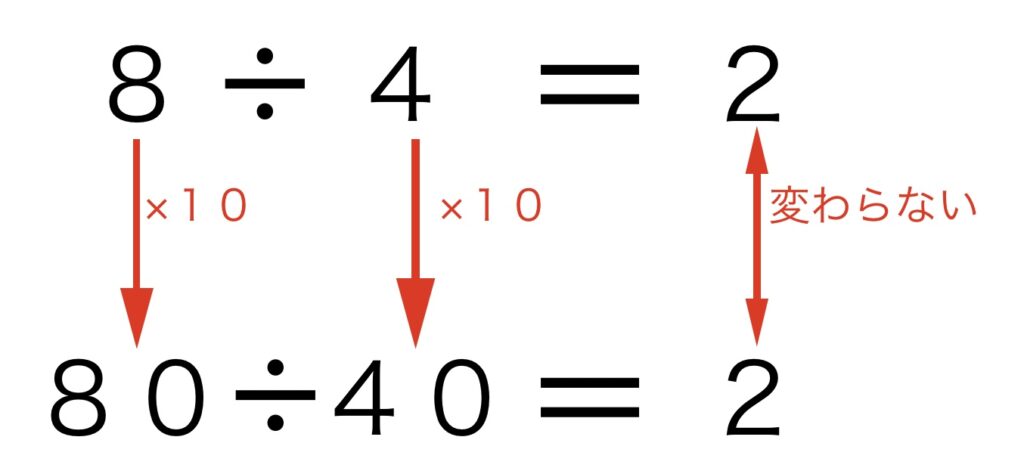
分母と分子をひっくり返して、かけ算をする理由
次の式を例にして説明ます。
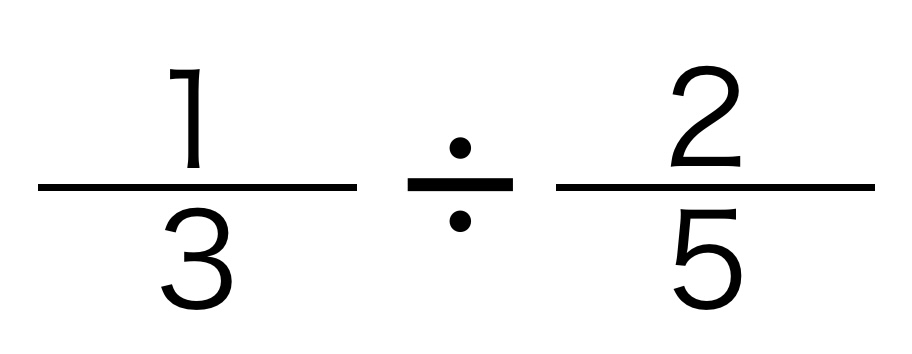
先ほど説明した「わり算の性質」である、わる数とわられる数に同じ数をかけます。
今回の式では、わる数2/5(5分の2)の逆数である5/2(2分の5)をかけます。すると以下のようになります。
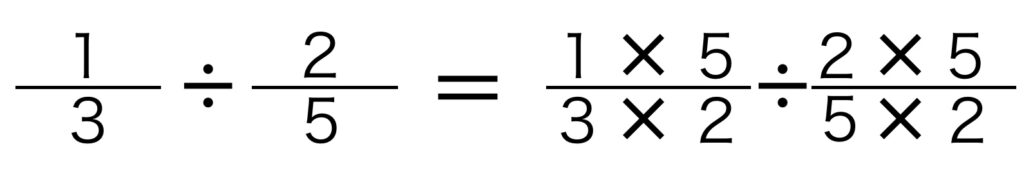
分数の割り算では、途中で約分ができるときは約分をしてから計算することが大切です。なので、ここで約分をします。約分をすると以下のようになります。
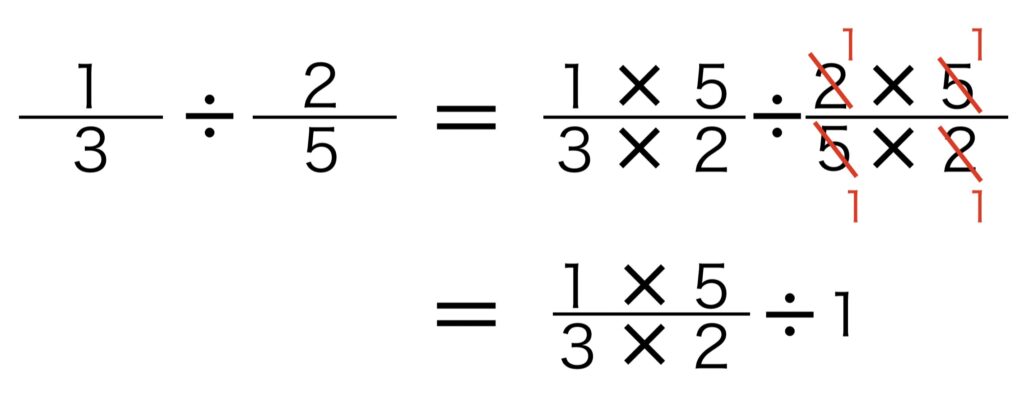
すると、どうでしょうか。
分数の割り算が分母と分子がひっくり返った掛け算に変わりました。
最後の「÷1」は、あってもなくても答えは変わりません。つまり、無視して計算してオッケーです。
ショートカットをしている
毎回正確な式を書くと、式が長くなってしまいます。
そのため、分数の割り算を計算するときはショートカットをしているとお考えください。このショートカットを表現する言葉が「分母と分子をひっくりかえす」ということです。
最後に
分数の割り算がなぜ分母と分子をひっくり返すのか、その理由を理解できたことと思います。
「公式を使えばいい」「計算ができたらそれでオッケー」を目標とせずに、しっかりと立ち止まり「なぜ?」を追求することで算数への理解が深まります。また、「なぜ?」を探求することは算数の楽しさを味わうことにも繋がります。
学校や家庭で算数を学ぶ際も「計算ができたらオッケー」とせずに「なぜ?」「どうして?」と深く考えることが大切です。
「知らないことを知る」ことは学習のモチベーションを高めるために効果的です。同時に、子供たちの中で「知っているつもり」を覆すことも、学習のモチベーションを高める上で効果的です。








コメント