「平均」大好き!
子どもたちは「平均」が大好きです。
というのも、何かあるとすぐに「平均が〜」「平均では〜」と考えます。当然、この考えも大切なのですが、あまりにも「平均」に頼りすぎているように感じます。これは子どもだけではなく、大人にも言えそうですね。世の中でこれだけ「平均」が浸透しているのは、やはりそれぐらい便利だからでしょう。もちろん私自身もよく使います。
しかし、「平均」がどのシチュエーションでも使える絶対的な考えなのかと言われれば、答えは「NO」です。平均には強みもあれば、弱みもあります。
そこで、今日の授業は「平均の脆さ」について触れていきます。
問題
のなごん君は1ヶ月のおこづかいが1200円だそうです。
しかし、のなごん君は「クラスの友達はもっとおこづかいをもらってるよ!」と言っています。
のなごん君の言い分は正しいと言えますか。あなたの意見をかきましょう。
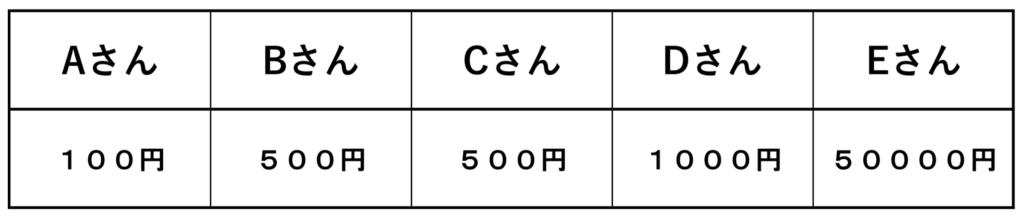
ポイント
感覚的に答えるのではなく、代表値(平均値、中央値、最頻値)を用いて答えることを大切にしましょう。きっと、こちらが何も言わなくても子どもたちは代表値を使って考えると思いますが、クラスの実態を見ながら場合によっては問題文に「代表値を使って」という条件を加えるとよいでしょう。
見通し

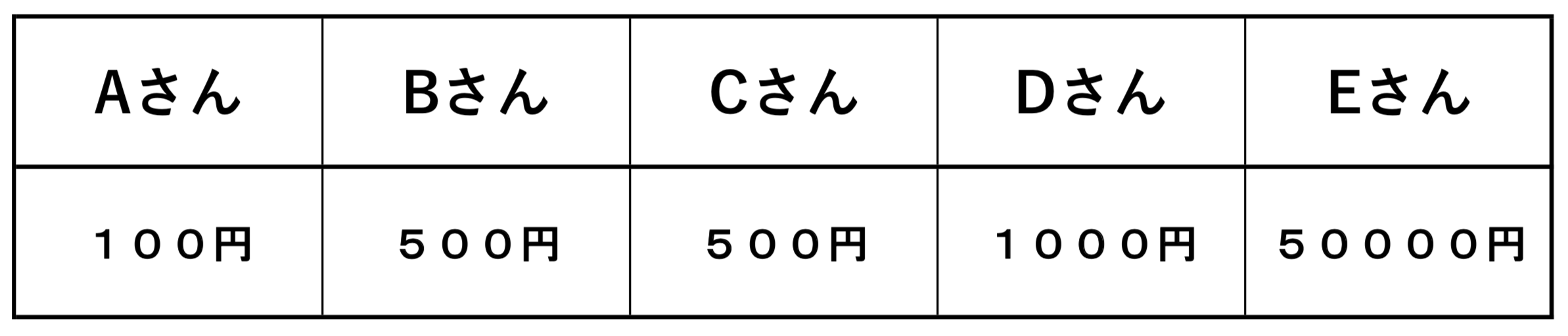
Eさん、おこづかいもらいすぎやろ!

500円が2人いる・・・

代表値を使って考えよう・・・
考え
最頻値
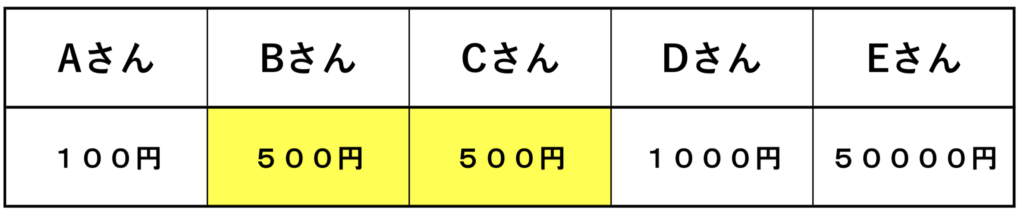
中央値
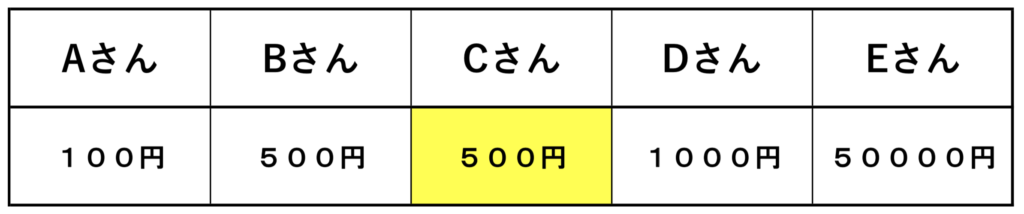
平均値
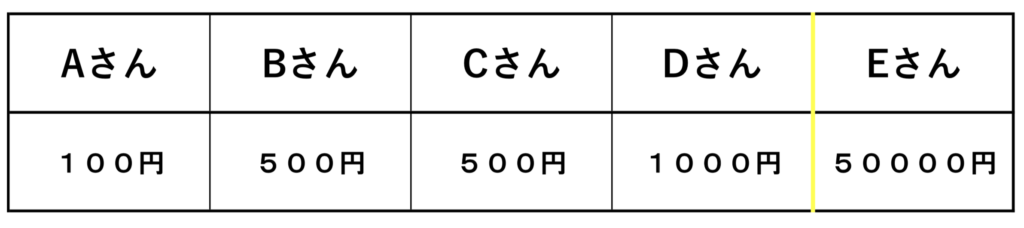
平均額・・・10420円
それぞれをまとめると・・・
最頻値・・・500円
中央値・・・500円
平均値・・・10420円
代表値から気づくこと
それぞれの代表値を見ると、平均値だけ極端に高いことに気づくはずです。
問題文に立ち返ると、「1200円よりもっともらっている」というのは正解とも不正解とも言えますが、大切なことは平均値だけで物事を判断しないということです。
この場合、平均値は10420円なので、1200円と比べるとたくさんもらっていると言えます。しかし実際は5人中4人は1200円より金額が少ないですし、最頻値も中央値も1200円より少ない結果となっています。
これらをトータルで判断して「どう考えるか」を学習の中で学ぶことは、日常生活においてとても役に立つスキルだと考えています。
おわりに
新しい知識を知ることは子どもたちにとって、楽しい学習と言えます。しかし、それだけが楽しい学習ではありません。
当たり前だと思っていたことを覆す学習も、知的に没頭できて楽しい学習となり得ます。
「平均」は極端な数(外れ値)に左右されやすいという特徴を知ることは、子どもたちにとって新たな価値が形成されると言えるでしょう。ただただ「平均」だけで物事を判断するのではなく、一度立ち止まって「平均って脆さもある・・・」「他の代表値なら・・・」と広い視点で物事を判断できる姿を期待しています。
学習前と学習後では、同じデータを見ても見方が変わったことを子どもたち自身が自覚できたなら、指導者としてこれ以上言うことはありません。





コメント