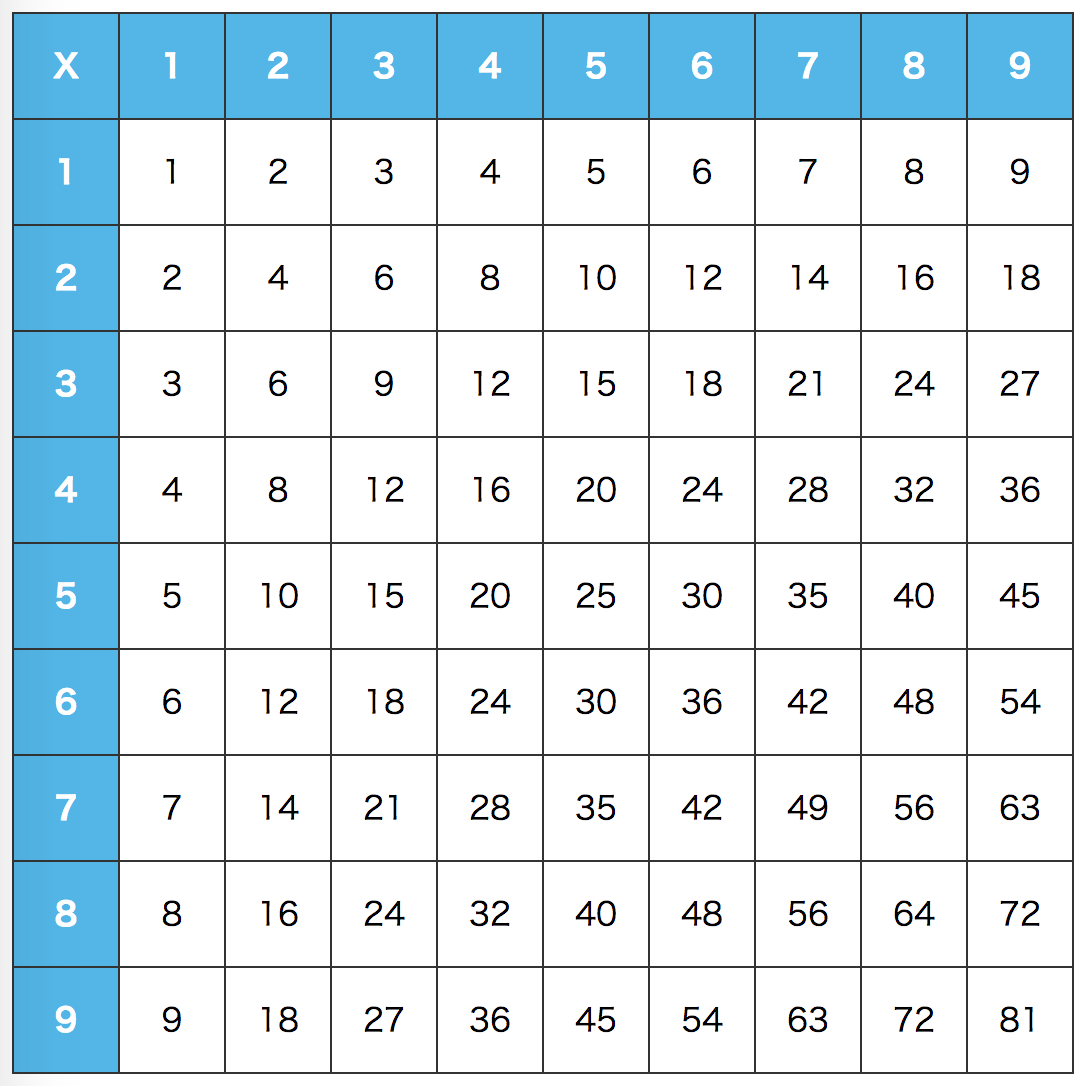
九九表
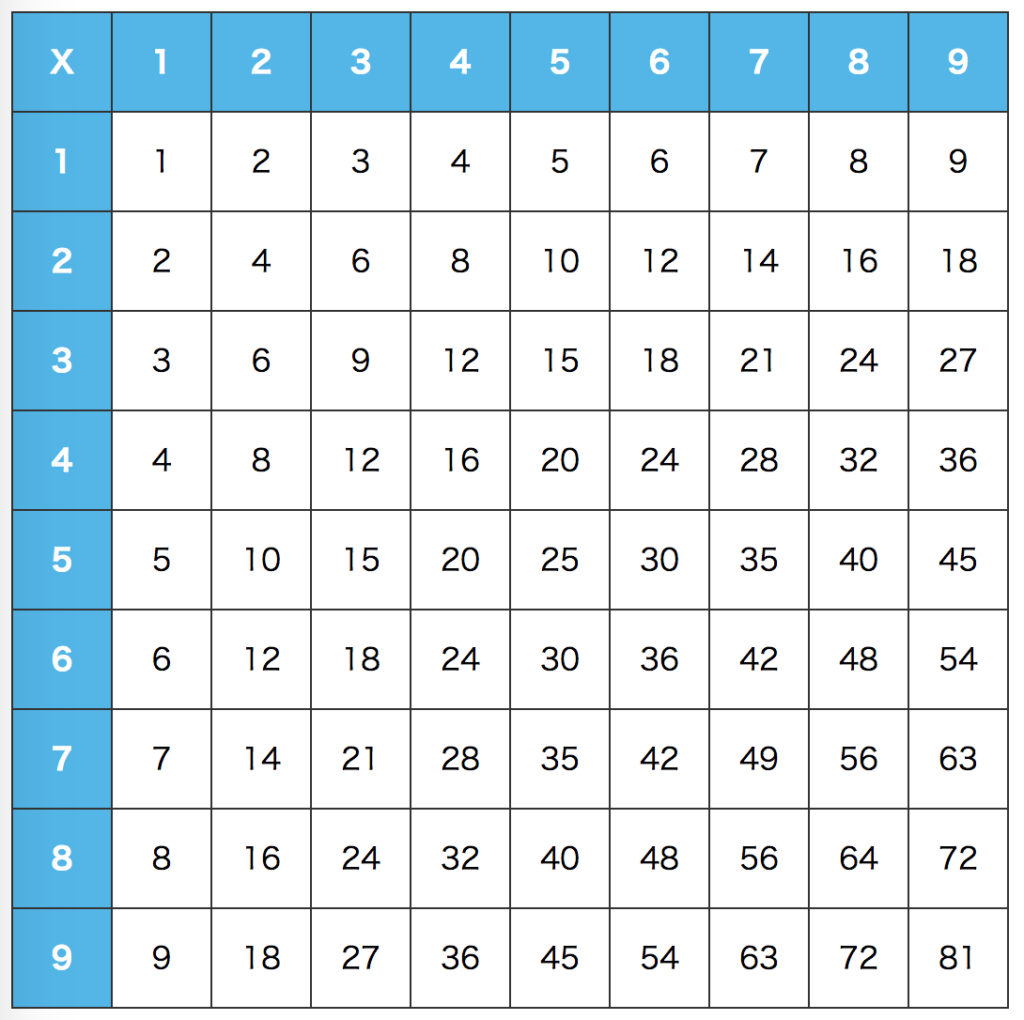
今回は九九表を使って学習を進めていきます。高学年に九九表は少し簡単なようにも思いますが、タイトルにもあるように「平均」の学習を取り入れることで程よい難易度となります。
最初は「簡単!」「出来そう!」と思えても、いざ問題に取り組むと「意外と難しい」「時間がかかる」と思うような課題だと思います。
また、課題自体の答えは1つですが、そこにたどり着くまでの方法は複数あります。子どもたちが、どのような方法で答えまでたどり着くのか。こちらが予想する方法以外の方法を生み出すのか。その辺りも指導者としては楽しみの1つと言えそうです。
導入


(1〜9までの表を掲示して)
平均はいくつでしょう。

全て足して9で割れば答えが出ます!

では、1度全て足して9で割る方法を使って平均を求めましょう。

(1+2+3+4+5+6+7+8+9)÷9=5
平均は5です。
ポイント
まずは、これまでに学習してきた平均を求める方法(合計÷個数)を使って考えさせましょう。理由は2点です。
・これまでの復習
・「計算が面倒」だと感じさせる
その上で他の方法を聞いていきます。きっと、子どもたちから「他の方法もある」「もっと簡単な方法がある」という声があがることでしょう。これらの声は後ほど「見通し」の時に聞いてあげるといいでしょう。
問題
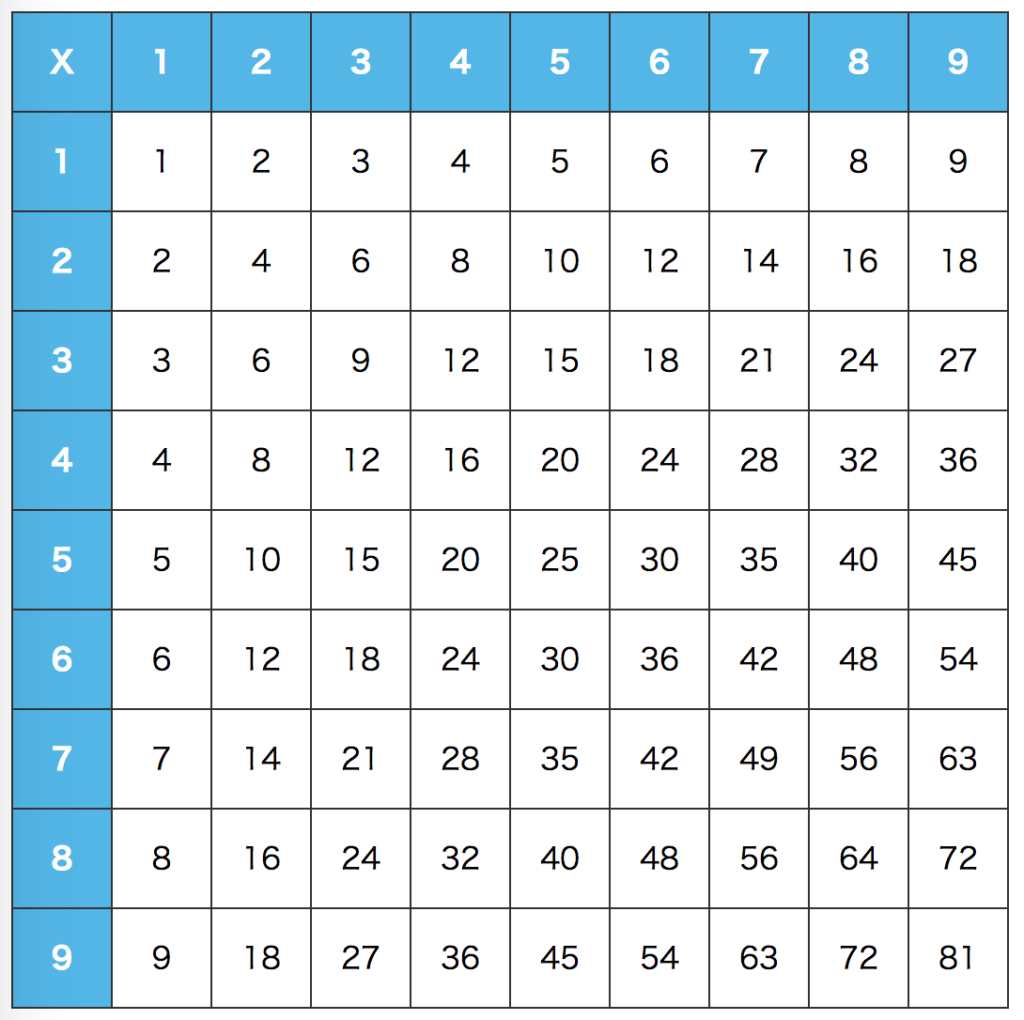
九九表の(白い部分の)平均はいくつでしょう。
見通し

全て足すのは大変ですね・・・

端と端の数を足せば簡単です!

端と端の数?Aさんが言っていることを説明できる人はいますか?

例えば1の段なら・・・
1+9=10、2+8=10、3+7=10・・・
このように計算を簡単にする方法(楽をする方法)を発見することでしょう。他にも方法はありますので、それは次の「考え」で記載します。実際の学習では、子どもたちの見通しをしっかりと聞いて、クラスで共有しましょう。
算数が苦手な子どもが多いクラスはここを丁寧にしてください。ここを疎かにすると教室中に「?」が蔓延します。反対に学力が高いクラスではここはサラッといっても構いません。あまり言い過ぎると考えることへのモチベーションが下がります。その辺りは、担任の先生が1番理解していると思いますので調整してください。
考え
順番に全て足す
1+2+3+4+5+6+7+8+9=45
2+4+6+8+10+12+14+16+18=90
以下9の段まで続ける。
端と端を足す
1+9=10、2+8=10、3+7=10、4+6=10、5+0=5・・・合計45
2+18=20、4+16=20、6+14=20、8+12=20、10+0=10・・・合計90
以下9の段まで続ける。
数を揃える
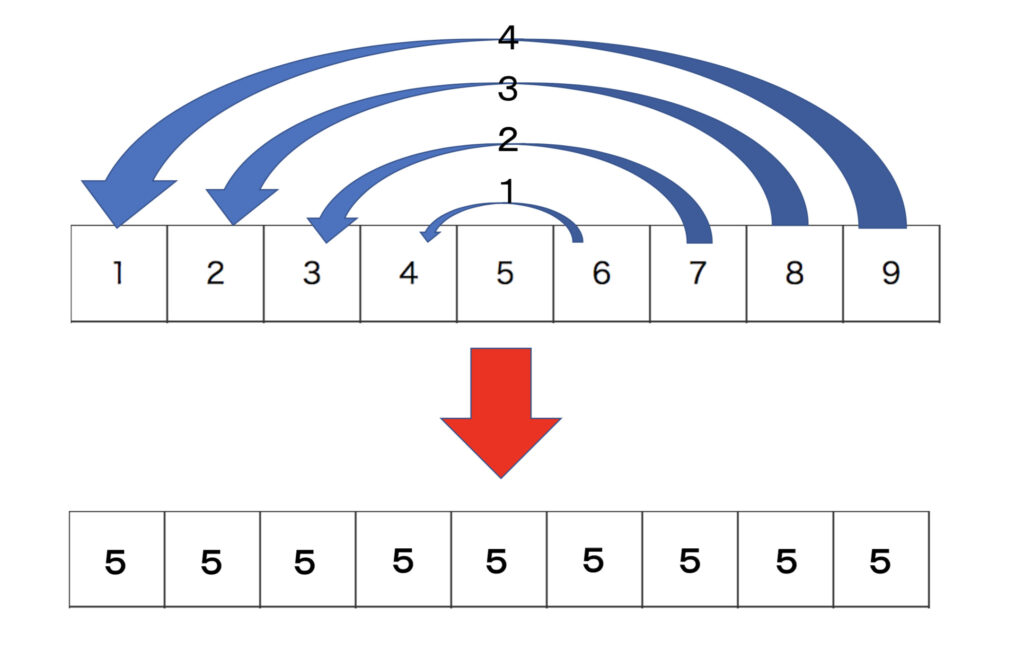
結論
九九表の合計・・・2025
九九表の平均・・・2025÷81=25
答え 25
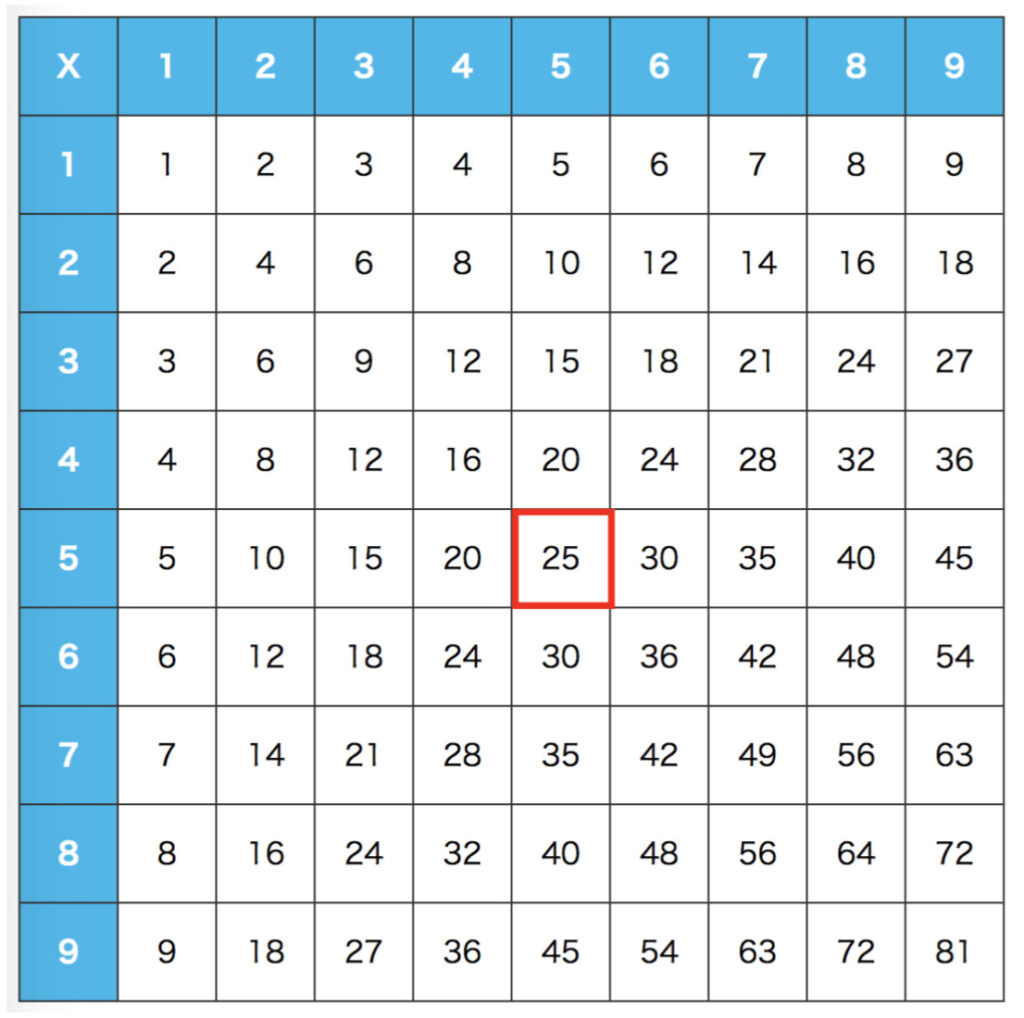

九九表の真ん中の数だ!
おわりに
本日紹介した方法は極々一部だと思います。きっとこれ以外の方法で考える子どもたちもいるでしょう。
今回の課題は、色んなアプローチで取り組むことができるので、きっと子どもたちも楽しく頭を働かせることだと思います。普通に考えると面倒な計算も、ほんの少し工夫をすることで楽に簡単に計算が出来るようになるというのは、算数の魅力の1つかもしれません。
高学年担任の先生方は是非1度試してみてください。飛び込み授業や研究授業でも可能な授業だと思います。





コメント