単元の目標
【知識・技能】
図や表などに表し落ちや重なりがないように、起こり得る場合を順序よく調べることができる。
【思考・判断・表現】
事象の特徴に着目し、順序よく整理する観点を決めて図や表などを用いたり、項目を記号に表したりして、順序よく筋道立てて考えている。
【学びに向かう力・人間力】
順序よく調べたことを振り返り、学習や生活に活用しようとしている。
指導計画(全7時間)
【第1次】組み合わせ(3時間)
【第2次】順列(2時間)
【第3次】場合の数を基にした確率(2時間)
本時の学習(第4時)
本単元は小学校学習指導要領解説算数編D(2)起こり得る場合にあたる。
ここでは、起こり得る場合を順序よく整理するための樹形図や二次元の表などの用い方について理解したり、順序よく整理する観点を決めたりし、落ちや重なりなく調べる方法を考察することを主なねらいとしている。
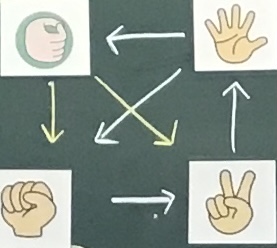
本時は子ども達にとって身近であろうジャンケンの「起き得るすべての場合の数」と「求める場合の数」について考える。
2人でグー、チョキ、パーの3種類でジャンケンをした際は9通りの場合が考えられる。その際、それぞれが勝つのは3通りずつ考えられ、あいこも3通りとなる。つまり、勝つ・負ける・あいこが1/3ずつということになる。
本時では実際に海外に存在する4種類の手があるジャンケンについて紹介し「4種類にすると、あいこになりにくいね」と問う。実際、あいこになるのは1/4であり、4種類のうち1種類は出す必要がなくなる。樹形図や図をかいて考えるなかで、実質3種類のジャンケンと同じことをしていることに気づかせたい。
その後、実際に存在する5種類のジャンケンを紹介し、あいこになるのは何通りかを考えさせる。ここでも樹形図や図を用いて考えさせるようにする。そして、5種類だと不要な手は存在せず、あいこになる可能性は下がる(決着がつきやすくなる)ことに気づかせたい。
そこから、「奇数種類だと不要な手は存在せず、あいこになりにくい?」「奇数種類だと早く決着がつくのかな?」ということに着目し、子ども達が自らすすんで考える姿を期待したい。
本時の目標
樹形図を用いて、あいこになる組み合わせについて考えることができる
本時の評価規準
樹形図を使い、あいこになる組み合わせについて考えている(思・判・表)
本時の展開
| ①本時の学習課題をつかむ。 | ・指導者と子どもでジャンケンを行う。この時、勝ち・負け・あいこを予想させることで、それぞれ何通りになるのかを考えさせる。 ・樹形図を使って考えさせることで、勝ち・負け・あいこはそれぞれ3通りあり、全部で9通りの出し方があることに気づかせる。 ・ジャンケンに新たに1手を加えると、あいこは何通りになるのかを問うことで、本時の課題を捉えられるようにする。 |
| ②あいこになるのは何通りかを自力解決する。 | ・樹形図を用いて起こり得る場合を全てノートにかかせることで、全部で16通りの出し方があり、その内あいこは4通りあることに気づくようにする。 |
| ③考えを共有する。 | ・4種類の出し方を整理して板書することで、グーを出す必要性がないということや、4種類のジャンケンでも実際は3種類で行なっていることに気づくようにする。 ・ ジャンケンの手が5種類の場合はどうなるかを問い、それぞれの手の関係が書かれたものを配布することで、5種類の場合を考えれるようにする。 ・5種類の出し方を整理して板書することで、不要な手がないことや、あいこになるのは1/5だということに気づくようにする。 |
| ④本時の学習を振り返る。 | ・本時の学習で気づいたことや考えたことを書かせることで、本時の学びを振り返らせる。 |






コメント