研究授業のド定番
L字型の面積を求める学習は、研究授業の中で最もよく見かける単元と言っても過言ではありません。実際に若い頃私も行ったことがありますし、何度も見たこともあります。
よく選ばれる理由としては「多様な考え方が生まれる」からだと思います。教科書の内容に沿って、そのまんま学習を進めても多様な考え方が生まれ、子どもたちもたくさん考えを述べるため、授業が流れていきます。そのため、授業者としては多くの人に見られる研究授業に選ぶのだと思います。
「教科書通りにしても上手くいくなら、それでええやん!」
NONONO!ちょっと待ってください。最後に隠し味を加えることで、さらに子どもたちの思考が深まります。

数値設定、条件設定、子どもたちへの指名方法の3つです!
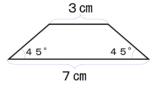
問題
面積は何㎠ですか。
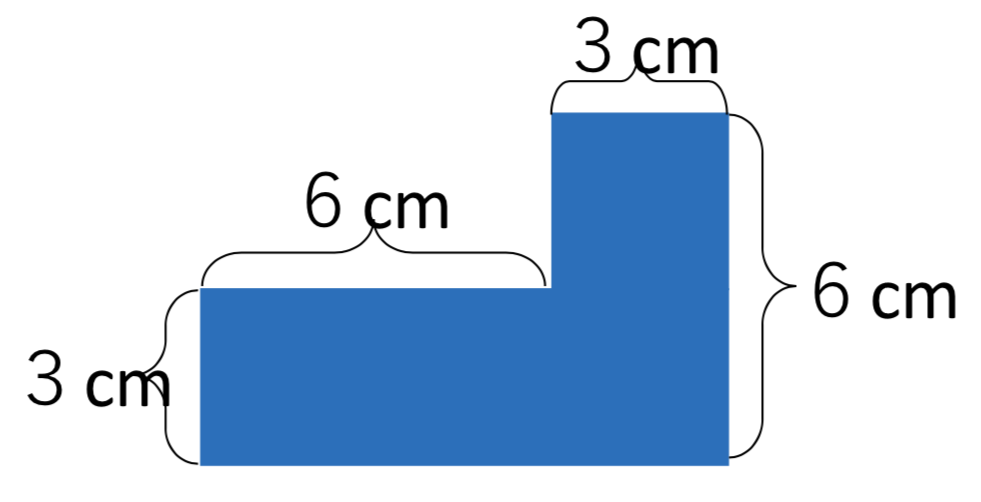
数値設定
教科書会社との数値設定とは少し変えています。この数値設定にすることで、より多様な考え方を引き出すことができます。大人の皆さんは、この問題を見て幾つの考え方ができますか?
条件設定
子どもたちへ問題を見せて、ただただ答えを考えましょうでは多様な考え方は出てきません。そこで条件として「3つ以上の考え方をノートに書きましょう」と伝えます。そうすることで、子どもたちの目的が「答えを導き出す」から「多様な考え方を導き出す」に変わるのです。1つ出来た子は2つ目、3つ目へと考えることで、空白の時間を無くすことにもつながります。
考え方
長方形と長方形に分ける
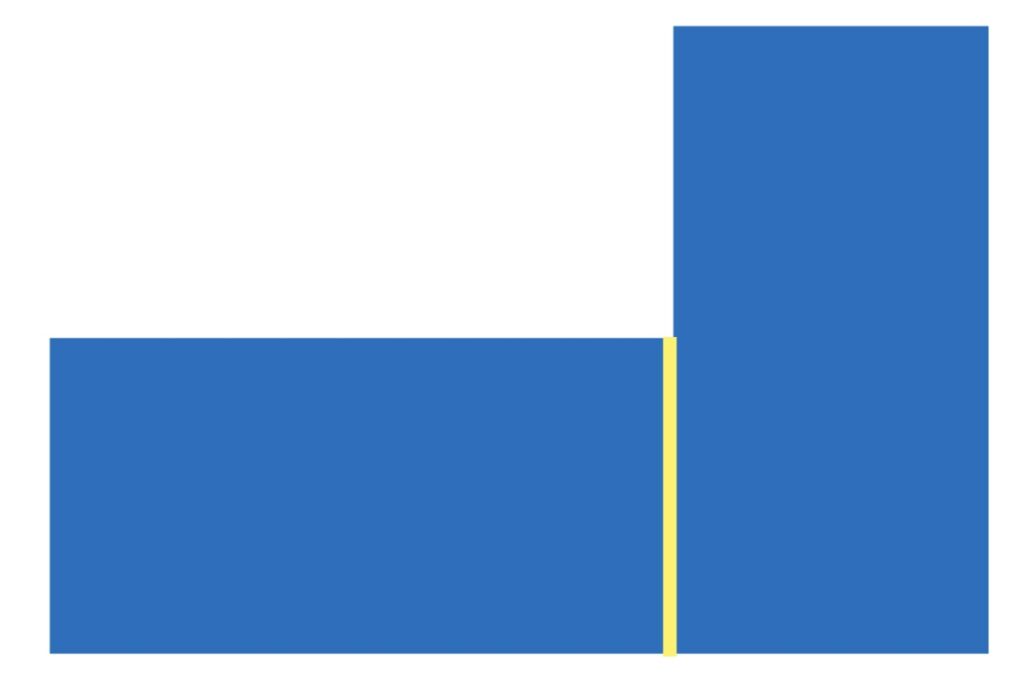
長方形と正方形に分ける

正方形に分ける
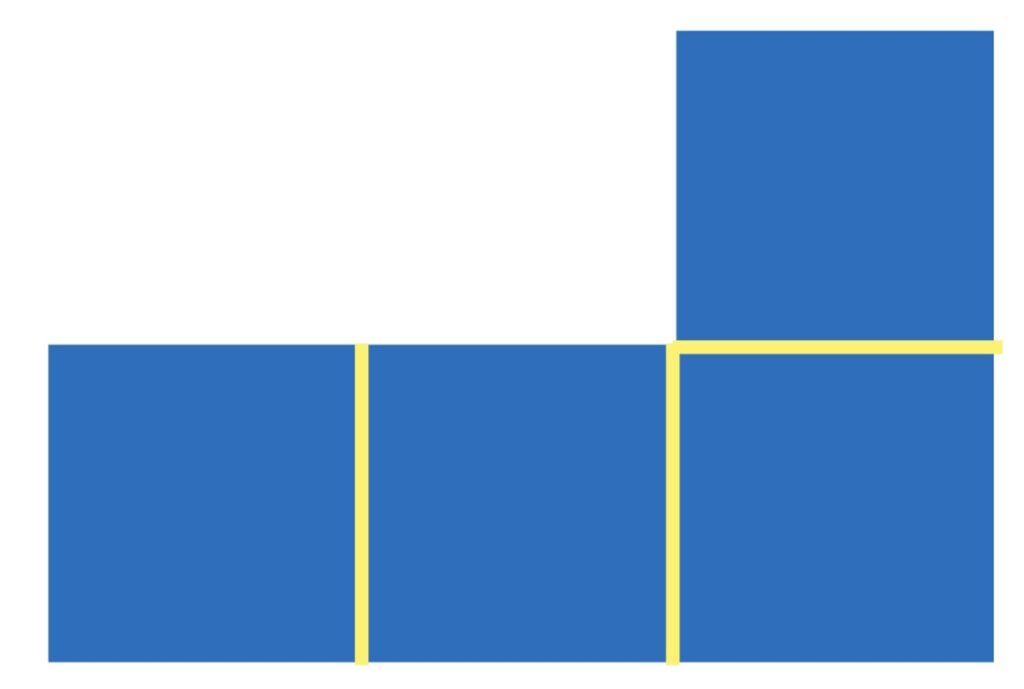
L字型を2つ合わせる(長方形にする)

L字型を2つ合わせる(ドーナツのようにする)

正方形を切って移動する(長方形にする)


数値設定を工夫することで、こんなにも多くの考え方が出ます!
指名方法で深める
隠し味の3つ目が、指名方法です。これについてはこの単元だけに留まらず、他の単元や他教科にも使える汎用的なものなので是非自分のモノにしてください。本当に使えます!
恐らく多くの指導者は一人の子どもが「図に表し」「式に表し」「説明をする」という3つを発表させる形式にしていると思います。しかし、この形式にすると友達の意見を聞く必要性がなくなってしまいます。そのため、発表している子どども以外の頭は働いていない状態になってしまっているのです。
そのような発表形式は言い換えるなら一人でドリブルをして、一人でゴールをしてしまっているのです。そこで、私が行っている方法は、細かくパスを繋ぐというものです。そう、バルセロナスタイルです。
図から式へ

どのような考え方をしたのか図に表してごらん。

私はこのように考えました。


じゃあ、このAさんの考えを式で言うとどうなるかな?

3×3=9

はいストップ!Bさんの続き言えるかな?

3×9=27

よし、これでオッケーですね!

違います!最後に9+27をしなくてはいけません!
式から図へ

どのような式で考えたのか教えてもらっていいかな

3×6=18

あー続きわかった!

じゃあAさんの続きを言ってもらっていいかな

3×6=18
18+18=36

じゃあ、この式を図に表すとどうなるかな?

はい、図に表すとこうなります。
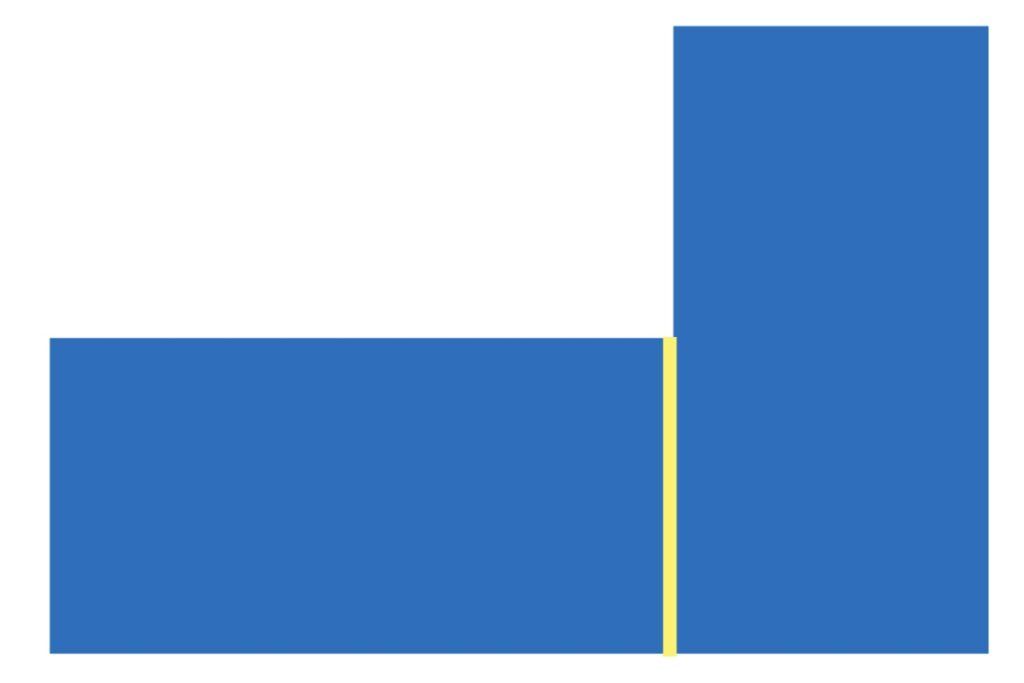
図と式の往還が理解を深める
このように算数の学習においては、図と式の往還が理解を深めることへと繋がります。
図を通じて問題や概念を視覚化し、それを式で表現することで抽象的な数学的思考を養うことができるのです。
子どもたちに丸投げしても、きっと子どもたちは図と式を往還させながら理解を深めていくことでしょう。しかし、指導者が意図的な指名方法を用いることで、さらに理解を深めることができます。また、友達の意見を聞く必要性も生まれるため、常に友達の意見に耳を傾けなくてはいけない状況が生まれるのです。
なので指導者が「友達の意見聞こうね!」と言わなくていい状況、つまり無駄な指導を減らすこともできるのです。ほんの少しの工夫でこれだけの良さがあります。
是非明日の算数の授業から取り入れてください。





コメント