場合の数
組み合わせについては6年生の「場合の数」で学習します。
今回は小学生には少し難しいかもしれませんが、野球の打順について触れてみましょう。小学生段階では計算によって答えを求めるのではなく、実際に書き出して試行することが大切です。
そのため、今回の学習内容を全て書き出すことは難しいかもしれませんが、題材としては子どもたちの興味を引き、学習意欲を高めることができると考えています。
打順
あるプロ野球の監督が、チームの主力メンバーは決まっているものの、打順の組み合わせに納得がいかないと頭を悩ませています。この問題を解決するために、日替わりで打順を変更し試してみることにしました。
しかし、全ての可能な打順を試すには、1日に1試合しか行えないと仮定した場合、何試合(何日)かかるのでしょうか。
侍ジャパン
侍ジャパンは、ほぼほぼ打順は固定でしたが、ここでは分かりやすいように侍ジャパンの決勝スターティングオーダーを使って説明していきます。
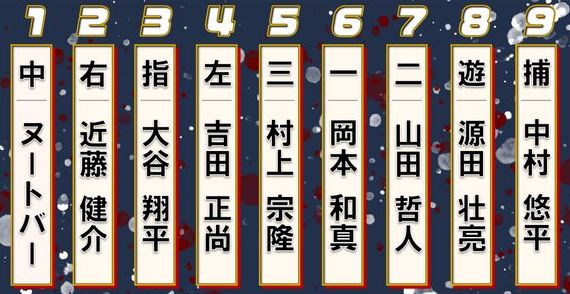
9人の打順は1番打者の候補が9通り(9人の候補)です。
仮に1番打者にヌートバー選手を選んだとします。
そうすると2番打者の候補がヌートバー選手以外の8通り(8人)です。
2番打者に近藤選手を選んだとします。
そうすると3番打者の候補がヌートバー選手、近藤選手以外の7通り(7人)です。
3番打者に大谷選手を選んだとします。
そうすると4番打者の候補がスートバー選手、近藤選手、大谷選手以外の6通り(6人)です。
これを繰り返して考えていくと・・・
9×8×7×6×5×4×3×2×1=36万2880
結論
選手9人の打順を全て試すには
36万2880試合
これを365日で割ると約994年かかる。
順列について
n個の中からr個を順番に選び出した場合の並べ方の総数を「順列」といいます。
nPrという記号で表します。
9人の打順を決めるということは、9人の中から9人を選んで順番に並べることと同じなので、
9P9と表すことができます。
9P9=36万2880
おわりに
上記の計算からわかるように、全ての可能な打順を試すには驚くべき数の試合が必要です。このチームが日替わりで打順を変えることになると、とんでもない年数を要します。
実際に試さなくても、算数の力を駆使して考えることは非常に有益です。今回の例だけでなく、様々な状況や課題に対して、事前に計算や論理的思考を活用することは、問題解決や意思決定において価値のあるスキルです。これも含めて算数を学習することは大切なことと言えそうです。









コメント