新幹線の座席
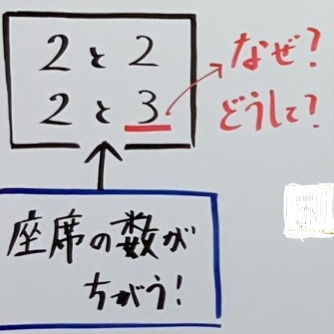
新幹線の座席が通常の電車と異なり「2席と3席」に分かれているのは、偶然ではなく必ず理由があります。今回の学習では、その理由に迫り、子供たち自身が新幹線の座席の秘密に迫っていきます。
この興味深いトピックに触れることで、子供たちは学習にワクワク感を持ち、夢中になり算数の学習へと取り組むことでしょう。
問題

新幹線の座席が「2席と3席」に分かれている理由はなんでしょう。
(2席と3席にすることの良さはなんでしょう)
※子どもたちとのやり取りの中で「どうして2席と3席なんだろう?」と疑問をもたせて、子どもたちの口から「どうして2席と3席なのかな」と言う流れでもっていけるといいですね。
見通し
「見通し」については目の前の子ども(クラス)の実態に応じて、かわってきます。
比較的算数を得意としている子どもたちが多いクラスなら、何も言わず取り組ませることもありでしょう。
反対に算数が得意でない子どもたちが多いクラスなら、しっかりと見通しをもたせてあげるべきでしょう。
難しすぎてもダメ。簡単すぎてもダメ。「しっかりと考えたら、できるかも?」ぐらいで子どもたちに取り組ませることが大切です。
例
3人で乗る場合、どうやって座るといいかな?
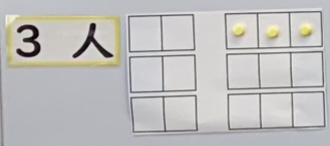
2人で乗る場合、どうやって座ればいいかな?

考え方
この問題に明確な答えは存在しません。最適解・納得解のみです。
ここでは例としていくつか掲載します。
2人以上なら何人で乗っても1人にはならない
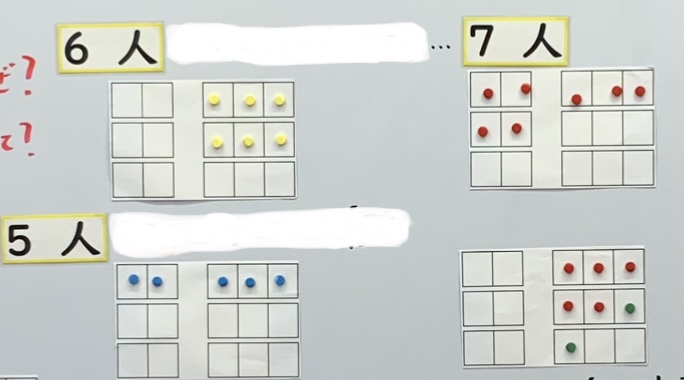
実際に試してもらえれば分かるんですが、2人以上なら「あまり1」は絶対に出ません。
子どもたちは図にかいたり、式に表したりと多様な表現で自分の考えを伝えようとするでしょう。
(そうなるように、こちらのファシリテートも大切になってきます)
【2の倍数】2、4、6、8、10・・・
【3の倍数】3、6、9、12、15・・・
【5の倍数】5、10、15、20、25・・・
上記の数値を組み合わせることで「あまり1」は出ないのです。

また、子どもたちによっては「2席と3席の場合、2席と2席と比べて、1度で多くの人数を乗せることができるから」と答えることもあるかと思いますが、それも否定することなくしっかりと受け入れることが大切です。
まとめ
2と3を組み合わせれば、1以外の全ての数をつくることができる!?
おわりに
まとめを「!?」で終わることで、子どもたちは自らすすんで実際に調べることでしょう。(過去に自分自身が受け持ったクラスは休み時間になっても、調べる子どもたちがたくさんいました)
このように、算数にのめり込む(没頭する)授業をすることが、私たち指導者として大切なことの1つだと思います。
日常に転がっている何気無い数字を授業として取り入れることで、子どもたちが日常生活の中にある「算数」を発見したり、疑問をもったりすることへとつながると信じています。







コメント