割合って?

6÷10=0.6(60%)
12÷20=0.6(60%)
18÷30=0.6(60%)
この単元では、割合を使って「シュートのうまさ」を比べる学習を行います。
教科書では「全シュート数」を基準量とし、その大きさを1として、それに対する「入ったシュート数」の割合を小数で表します。これにより、シュートの成功率を数値で比較することができます。
今までは「差」を使って数値の比較をしてきましたが、この単元では「割合」を使った比べ方を学んでいきます。
しかし、実際の生活場面では「割合」だけでは解決できない場面が多くあります。
そこで、今回は数値や表を工夫することで「割合」だけでは解決できない問題に取り組んでいきます。
問題
あなたはサッカーチームの監督です。
PKを蹴る選手を、あと1名決めなくてはいけません。
4人の中で誰を選びますか。
ポイント
今回は一度に全ての数値を提示するのではなく、少しずつ提示していきます。そうすることで、子ども達が必要な数値に気づけるようにします。
見通し


(表を掲示して)
こうやって見ると、これまでにB選手が最もPKを決めているので、B選手でよさそうですね!

これまでに何本蹴ったかが分からないと比べることができません。

もしかするとB選手の失敗も1番多いかもしれません!

これまでに蹴った数や、失敗の数が分かればいいんですね。
既習事項と関連づける
このようなやり取りを挟むことで、「割合」で比べるという見通しをもたせることができます。
考え
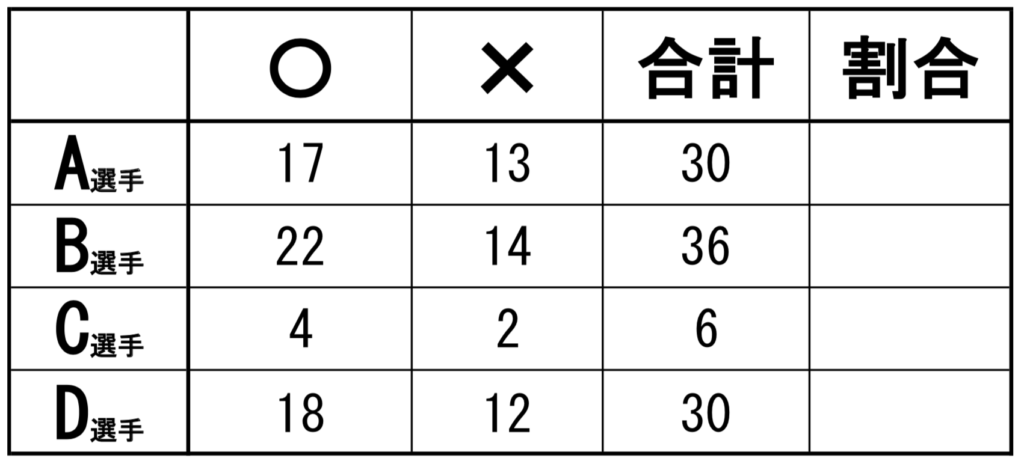
A選手・・・17÷30=約0.57
B選手・・・22÷36=約0.61
C選手・・・4÷6=約0.67
D選手・・・18÷30=0.6
完成した表
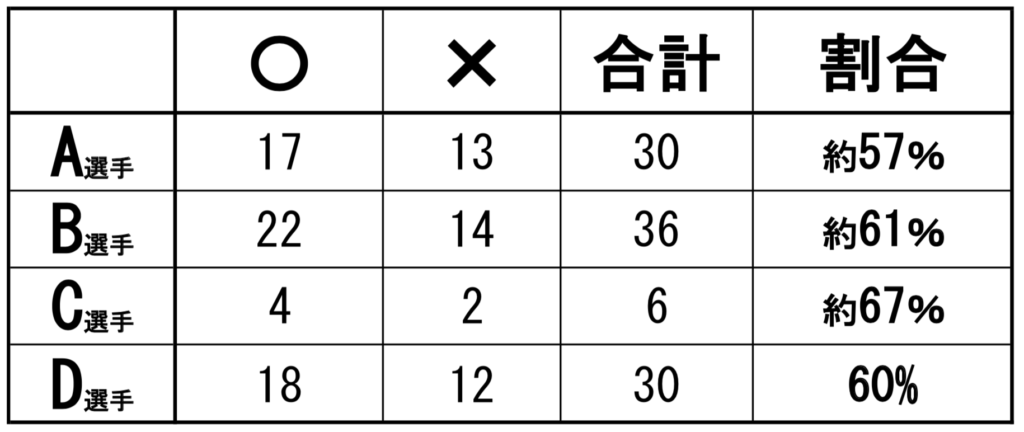
割合だけで決めていいの?

C選手が最も成功率が高いので、C選手で良さそうですね!

でも、今までに6本しか蹴っていません・・・

B選手は61%だけど、今までに36本も蹴っていて経験が豊富です。
このように、割合以外の数値も着目した発言が出ることだと思います。そういった発言が出たら、さらに揺さぶりをかけていきます。
これまでのデータを掲示する
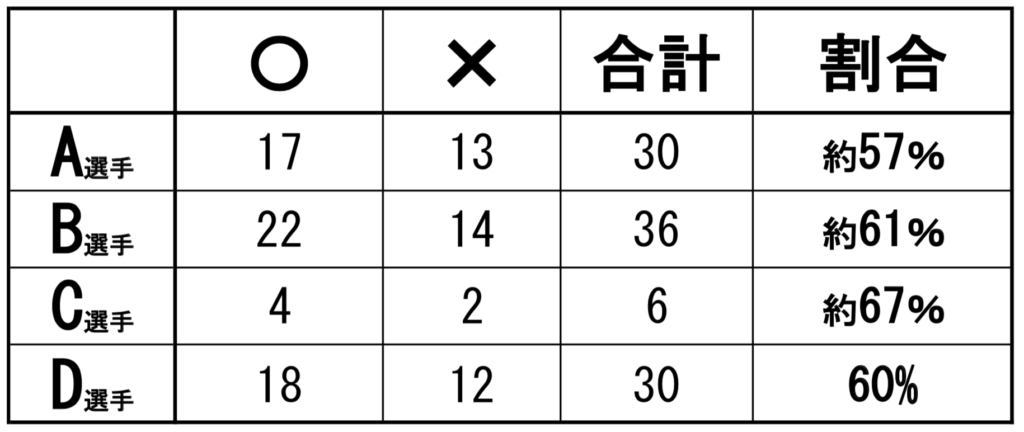

【重要】全体の割合以外にも着目する
・過去5回に入った割合(調子の良さ)
・最も良い区間の割合
・安定感
・試行回数
など
何を重要視するか
リアルな日常生活では、割合だけで物事を決めることができません。もちろん、割合という見方をすることは大切ですが、それが全てだと思ってはいけません。
あらゆる数値を総合的に判断して、物事は決定していきます。
その中で「何を重要視するのか」といった経験を授業に取り入れることで、算数と日常生活のつながりに気づいたり、日常生活の中で算数を使う姿へとつながっていくように思います。
ただただ機会的に「割合で比べればいい」で留まるのではなく、「割合は数ある判断材料の中の1つ」ということまで踏み込むことも大切なことだと考えています。






コメント