台形の面積
以前、高さがわからない台形の求積問題をご紹介しましたが、今回はオーソドックスな台形の求積問題に取り組みます。このような教科書通りの内容を、楽しく分かりやすく展開することは、指導者としての重要なスキルです。
今回は、「条件設定」「配布教材」「指名方法」の工夫に注力し、子どもたちが楽しみながら理解を深められる授業をデザインします。
問題
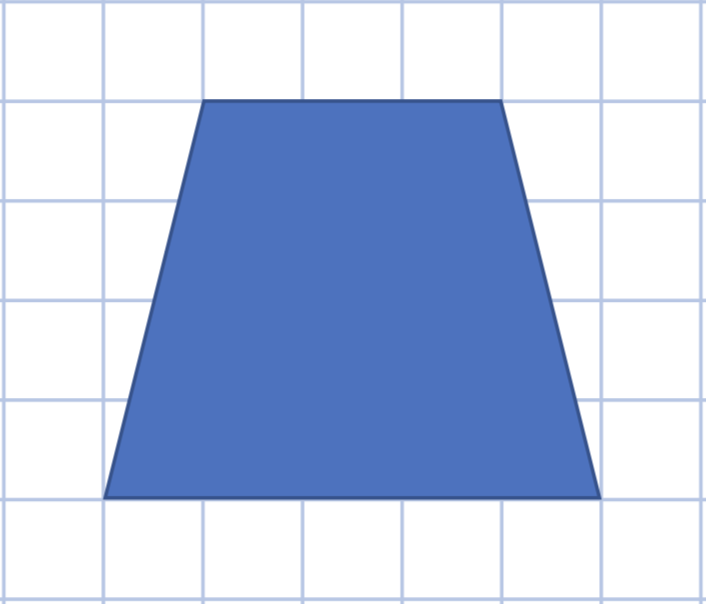
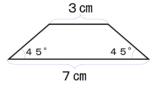
面積は何㎠ですか。
3つの方法を使って分かりやすく説明しましょう。
ポイント①(条件設定)
答えを導くことが目的ではなく、問題をしっかりと説明する力を養うことが焦点です。この能力を磨くには、問題の本質を深く理解することが欠かせません。また、分かりやすく説明するためには、自分の文章を客観的に評価するスキルも重要です。
加えて3つの方法を考えさせることで、即座に完了するのではなく、問題の解決に真剣に取り組む姿勢が養われます。また、他にどのようなアプローチが考えられるかを探求することも促されます。子どもたちの深い思考と説明力を引き出す機会となるでしょう。
ポイント②(配布教材)
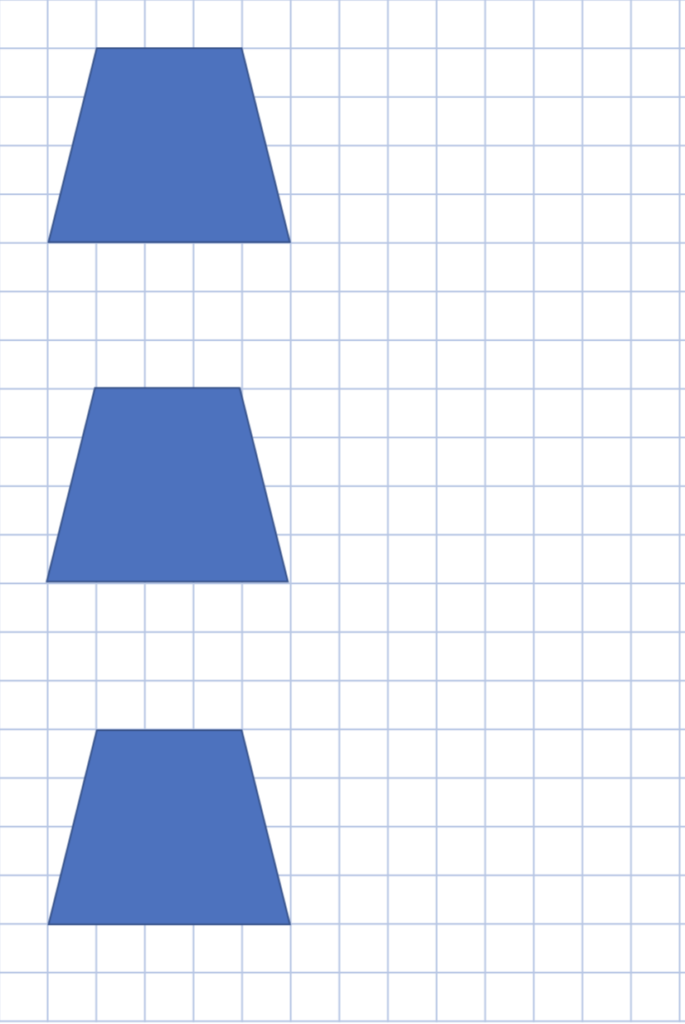
配布物は、縦に3つ繋がっている形で提供しましょう。これにより、子どもたちのアイデアを図の右側に描き込むことができます。
説明をノートに記す際は、「図・式・言葉」を活用して説明することを心掛けさせましょう。既に4月から継続してこのアプローチを伝えているなら、子どもたちも自然と図や式を使う習慣が身についていることでしょう。ただ、この習慣がまだ身についていない場合は、指導者の方から積極的にアプローチを行い、サポートしていくことが大切です。
考え
台形を2つならべる
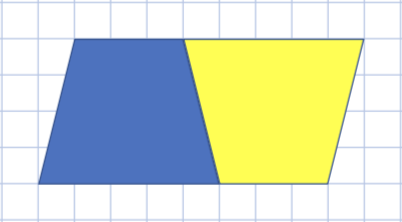
(5+3)×4÷2=16
答え16㎠
平行四辺形にする
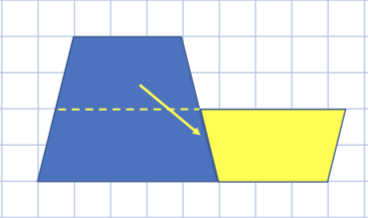
(5+3)×2=16
答え16㎠
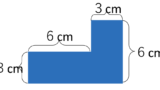
正方形にする
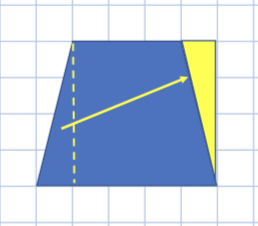
4×4=16
答え16㎠
対角線で2つの三角形に分ける
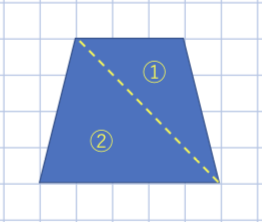
①3×4÷2=6
②5×4÷2=10
10+6=16
答え16㎠
ポイント3(指名方法)
図から式
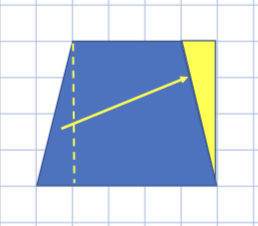

この図はAさんがかいたものです。Aさんの考えを式に表すとどうなりますか?

4×4=16
式から図

(3×4÷2)+(5×4÷2)

Bさんの考えを図に表すとどうなるでしょう?
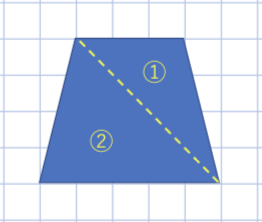

(図をかく)
このようになります。
まとめ
台形の面積を求めるときは、切ったり、くっつけたりして他の形に変えるとよい。
(子どもの言葉でまとめてください)
おわりに
今回のように問題の本質を理解し、説明するスキルを養うことで、子どもたちは深い思考力と説明力を身につけることができます。配布教材を使いながら「図・式・言葉」をうまく活用し、問題を理解しやすく説明することを意識させましょう。
さらに、指名方法を通じて子どもたちが自ら考え、他者のアプローチも理解する機会を提供しましょう。これによって、楽しみながらも本質的な学びが促進され、より深い理解が生まれるでしょう。
ほんの少しの工夫が子どもたの学びを深めることでしょう。





コメント